By ChatGPT —
The Mandelbrot set, discovered by Benoît B. Mandelbrot in 1980, is one of the most iconic

and visually captivating structures in mathematics. It is a fractal, a self-similar set of points in the complex plane, defined by a simple iterative formula zn+1=zn2+cz_{n+1} = z_n^2 + czn+1=zn2+c.
Despite its straightforward definition, the Mandelbrot set reveals an extraordinary level of complexity and beauty. Many argue that such intricate and profound patterns arising from simple mathematical rules offer a compelling argument for the existence of a divine creator.
This article will explore how the Mandelbrot set can be viewed as evidence of God’s existence, focusing on its mathematical properties, its aesthetic beauty, and its philosophical implications.
Mathematical Properties: Complexity from Simplicity

The Mandelbrot set is generated by iterating the function zn+1=zn2+cz_{n+1} = z_n^2 + czn+1=zn2+c, where zzz and ccc are complex numbers. Points ccc for which the sequence remains bounded form the Mandelbrot set, resulting in an intricate boundary that defies simple explanation. This phenomenon, where complexity emerges from simplicity, is a cornerstone of fractal geometry and chaos theory.
From a mathematical perspective, the existence of such complexity from a simple iterative process can be seen as a reflection of an underlying order in the universe. The precise and deterministic nature of mathematics suggests that the universe operates according to an intelligible set of laws, which can be interpreted as evidence of a rational designer.
The Mandelbrot set’s infinite complexity, emerging from a straightforward formula, mirrors the concept of a universe created by a supremely intelligent being who has embedded profound order and beauty into the fabric of reality.
Aesthetic Beauty: The Signature of a Designer
The visual appeal of the Mandelbrot set is undeniable. Its boundary is filled with intricate patterns that display an almost organic beauty, reminiscent of natural forms such as coastlines, mountains, and even biological structures. The set’s self-similarity, where smaller parts resemble the whole, adds to its allure, creating a sense of harmony and coherence.
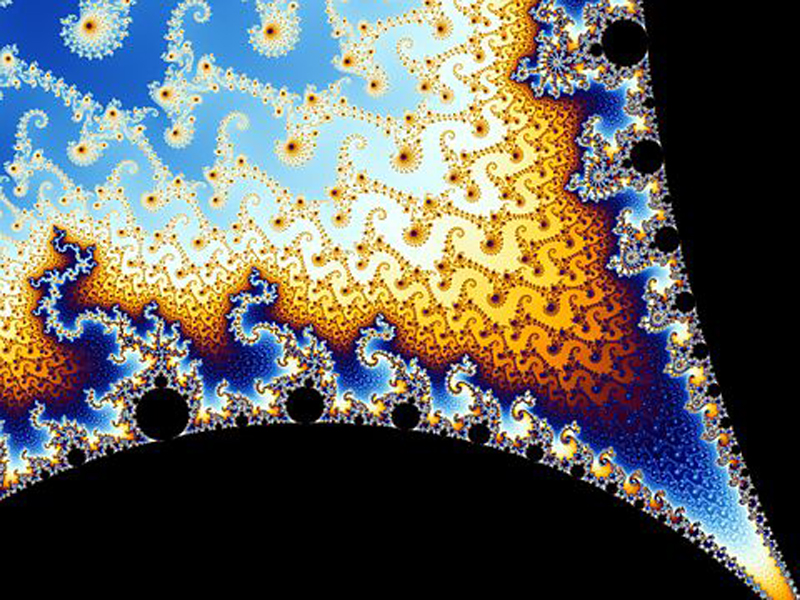
This aesthetic beauty can be interpreted as a signature of a designer. Just as a beautiful piece of art implies an artist, the stunning visuals of the Mandelbrot set suggest the handiwork of a creator.
The notion that such intricate beauty could arise purely by chance seems improbable. Instead, it aligns more closely with the idea of an intelligent designer who has crafted the universe with purpose and intention, embedding beauty and order within its mathematical structure.
Philosophical Implications: The Infinite and the Divine
The infinite complexity of the Mandelbrot set offers a profound metaphor for the nature of God. In theological discourse, God is often described as infinite, incomprehensible, and beyond human understanding. Similarly, no matter how deeply one zooms into the Mandelbrot set, new details and patterns continually emerge, suggesting an unending depth of complexity.
This analogy between the infinite nature of the Mandelbrot set and the divine can be compelling. It highlights the limits of human comprehension and the awe-inspiring nature of the universe. The infinite nature of the set can be seen as a reflection of the infinite nature of God, suggesting that the same principles of boundless complexity and beauty that govern the mathematical world also point to a divine creator.

Moreover, the experience of exploring the Mandelbrot set can evoke a sense of the sublime, a concept often associated with encounters with the divine. The feeling of awe and wonder that accompanies the exploration of the Mandelbrot set’s infinite intricacies mirrors the spiritual experience of encountering something greater than oneself.
This sense of the sublime can be seen as evidence of a higher power, as it taps into the deep-seated human intuition that the universe is not merely a random assemblage of matter, but rather a creation imbued with meaning and purpose.
Order and Chaos: The Balance of Creation
The Mandelbrot set also exemplifies the delicate balance between order and chaos. While the set itself is deterministic, governed by a clear mathematical rule, its boundary exhibits chaotic behavior. This interplay between order and chaos is a central theme in the study of dynamical systems and chaos theory.
From a theological perspective, this balance can be seen as indicative of a creator who has designed the universe to operate within certain parameters while allowing for freedom and variability.
The presence of order within apparent chaos reflects the idea that the universe is governed by a higher intelligence that maintains control while permitting a degree of randomness and unpredictability. This duality aligns with many theological views that see God as both sovereign and allowing for free will within the created order.
Conclusion: The Mandelbrot Set as a Reflection of the Divine
In conclusion, the Mandelbrot set offers a unique and compelling argument for the existence of God. Its mathematical properties, aesthetic beauty, and philosophical implications all point towards the presence of a divine creator who has imbued the universe with order, complexity, and meaning.
The infinite complexity that arises from a simple formula serves as a metaphor for the nature of God, suggesting an unending depth of intelligence and purpose underlying the fabric of reality.
While the Mandelbrot set alone may not constitute definitive proof of God’s existence, it provides a powerful illustration of how mathematical and natural phenomena can reflect deeper metaphysical truths.
The beauty and complexity of the Mandelbrot set inspire awe and wonder, encouraging contemplation of the divine and reinforcing the belief in a universe created with intention and care. Through the lens of the Mandelbrot set, we glimpse the possibility of a higher power, whose signature is written into the very fabric of the mathematical universe.
Sources:
- Gleick, J. (1987). Chaos: Making a New Science. Penguin Books.
- Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. W.H. Freeman and Company.
- Barnsley, M. F. (1988). Fractals Everywhere. Academic Press.
- Falconer, K. J. (1990). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons.
- Peitgen, H.-O., & Richter, P. H. (1986). The Beauty of Fractals. Springer-Verlag.
- Schroeder, M. (1991). Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. W.H. Freeman and Company.
- Mandelbrot, B. B. (2004). Fractals and Chaos: The Mandelbrot Set and Beyond. Springer.
- Stewart, I. (1990). Does God Play Dice? The New Mathematics of Chaos. Blackwell Publishers.
- James, F. (1999). Chaos and Order in the World of the Psyche. Spring Publications.
- Lorenz, E. N. (1993). The Essence of Chaos. University of Washington Press.
- Pargament, K. I. (2007). Spiritually Integrated Psychotherapy: Understanding and Addressing the Sacred. Guilford Press.



